Informed search strategies make use of problem-specific knowledge beyond the sole definition of the problem (i.e., the adjacency matrix of the graph), and take advantage of it to find solutions more efficiently than uninformed search strategies. The general informed search approach is called best-first search (BES). According to this method, a node must be selected for expansion based on an evaluation function (i.e., a cost estimate). In this sense, a heuristic function is the most common form to add knowledge into the BES algorithm. The heuristic indicates the estimated cost of the cheapest path from the present state to the goal state. Thus, the BES implementation is like uniform-cost search (UCS) but using a heuristic (node-wise vector) and an evaluation function (given as a handle) instead of the default accumulated path cost, see Figure 1.
Figure 1. Best-first search algorithm.
## @deftypefn {Function File} {@var{solution} =} best_first_search (@var{problem}, @var{start}, @var{finish}, @var{treegraph}, @var{feval}, @var{heuristic})
## Best-first search algorithm.
##
## PRE:
## @var{problem} must be the cost-weighted adjacency matrix.
## @var{start} must be the starting node index.
## @var{finish} must be the finishing node index.
## @var{treegraph} must be the tree/graph version flag. 0 is tree-version.
## @var{feval} must be a handle to the evaluation function.
## @var{heuristic} must be a heuristic at the node level.
##
## POST:
## @var{solution} is the solution path. State set to zero if failure.
##
## In this implementation, cost is a vector: [path_cost heuristic_cost].
## @end deftypefn
## Author: Alexandre Trilla <alex@atrilla.net>
function [solution] = best_first_search(problem, start, finish, ...
treegraph, feval, heuristic)
% inits
node.state = start;
node.parent = [];
node.cost = [0 heuristic(start)];
if (node.state == finish)
solution = node;
else
frontier = [node];
explored = [];
found = 0;
while (~found)
if (numel(frontier) == 0)
solution.state = 0;
found = 1;
break;
endif
% pop frontier, lowest cost node
testNode = frontier(1);
testIdx = 1;
for i = 2:numel(frontier)
if (feval(frontier(i).cost) < feval(testNode.cost))
testNode = frontier(i);
testIdx = i;
endif
endfor
frontier = ...
frontier([1:(testIdx-1) (testIdx+1):numel(frontier)]);
node = testNode;
% check
if (node.state == finish)
solution = node;
break;
endif
% explore
if (treegraph)
explored(numel(explored)+1) = node.state;
endif
for i = 1:size(problem, 2)
if (problem(node.state, i)>0)
if (i ~= node.state)
child.state = i;
child.parent = [node.parent node.state];
accumPath = node.cost(1) + problem(node.state, i);
child.cost(1) = accumPath;
child.cost(2) = heuristic(i);
notExpl = 1;
if (treegraph)
notExpl = ~sum(explored == i);
endif
if (notExpl)
inFront = 0;
for j = 1:numel(frontier)
if (frontier(j).state == i)
inFront = 1;
if (feval(frontier(j).cost) > feval(child.cost))
frontier(j) = child;
endif
break;
endif
endfor
if (~inFront)
frontier = [frontier child];
endif
endif
endif
endif
endfor
endwhile
endif
endfunction
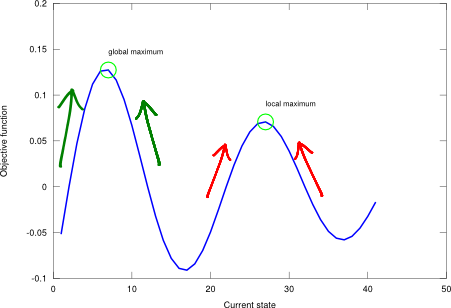
Note that the heuristic operates at the node level (not at the path level like a step cost). It’s a state fitness function and it doesn’t add-up over the traversal of nodes. With a good heuristic function, the complexity of the search procedure can be reduced substantially. The amount of the reduction, though, depends on the particular problem at hand and on the quality of the heuristic. And there is no free lunch here: developing a bespoke solution for a specific problem entails carefully designing a tailored heuristic, which generally works well only for this particular scenario.
A good heuristic never overestimates the number of steps to the solution. This requirement is commonly known as “admissibility”. In order to comply with it, the heuristic usually represents the cost of an optimal solution to a relaxed problem, which is the original problem without some constraints. Additionally, a heuristic may also show “consistency” if its estimated cost is monotonically non-increasing as it approaches the goal state (this is a stronger condition). As a rule of thumb, it is generally better to use a heuristic function with higher values provided it is consistent and that its computation is short.
Greedy search in detail
Greedy search (GS) is an informed search method that tries to expand the node that is strictly closest to the goal, assuming that it is likely to lead to a solution quickly. Thus, it evaluates neighbouring nodes by using only the heuristic function. Note that GS is not optimal nor complete (the immediate short-term benefit may not be the optimum one in the long run), but it is often efficient. Regarding its implementation, the former BES procedure is used with an anonymous evaluation function that returns the heuristic alone , see Figure 2.
Figure 2. Greedy search algorithm.
## @deftypefn {Function File} {@var{solution} =} greedy_search (@var{problem}, @var{start}, @var{finish}, @var{treegraph}, @var{heuristic})
## Greedy search algorithm.
##
## PRE:
## @var{problem} must be the cost-weighted adjacency matrix.
## @var{start} must be the starting node index.
## @var{finish} must be the finishing node index.
## @var{treegraph} must be the tree/graph version flag. 0 is tree-version.
## @var{heuristic} must be the heuristic vector.
##
## POST:
## @var{solution} is the solution path. State set to zero if failure.
## @end deftypefn
## Author: Alexandre Trilla <alex@atrilla.net>
function [solution] = greedy_search(problem, start, finish, treegraph,
heuristic)
% eval func is anonymous and returns heuristic
solution = best_first_search(problem, start, finish, treegraph, ...
@(cost) cost(2), heuristic);
endfunction
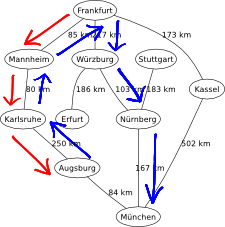
Following the UCS example with the graphical map of Germany, the heuristic of use for GS is based on the distance to München by motorways provided by ViaMichelin (a close resemblance to a straight-line distance). The resulting path from Frankfurt to München is the same, via Wurzburg and Nurnberg. However, GS resolves the problem in 6.96ms, while UCS does it in 12.4ms (almost double the time). Indeed, GS is more effective than UCS finding the best path in this informed environment.