The recursive best-first search (RBFS) algorithm is a simple recursive algorithm that attempts to mimic the operation of A-star search (i.e., the standard best-first search with an evaluation function that adds up the path cost and the heuristic), but using only linear space (instead of showing an exponential space complexity). The structure of RBFS is similar to that of recursive depth-first search (a tree-search version), but rather than continuing indefinitely down the current path, it uses an evaluation limit to keep track of the best alternative path available from any ancestor of the current node, see Figure 1.

Figure 1. RBFS applied on the graphical map of Germany, from Frankfurt to München.

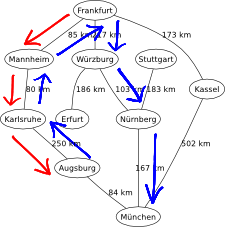
RBFS is robust and optimal (if the heuristic is admissible), but it still suffers from excessive node regeneration due to its low memory profile, which entails a long processing time. Given enough time, though, it can solve problems that A-star cannot solve because it runs out of memory.

Figure 2. Recursive best-first search algorithm.

-- Recursive best-first search algorithm.
--
-- PRE:
-- problem - cost-weighted adjacency matrix (table).
-- start - starting node index (number).
-- finish - finishing node index (number).
-- heuristic - must be a heuristic at the node level (table).
--
-- POST:
-- solution - solution path (table). State set to zero if failure.
--
-- In this implementation, cost is a vector:
-- {path_cost, heuristic_cost}.

function recursive_best_first_search(problem, start, finish,
  heuristic)
  -- inits
  local node = {}
  node.state = start
  node.parent = {}
  node.cost = {0, heuristic[start]}
  return rbfs(problem, node, finish, heuristic, math.huge)
end

function rbfs(problem, node, finish, heuristic, flimit)
  if (node.state == finish) then
    return node
  else
    local successors = {}
    -- for each action in problem given state...
    for i = 1, #problem do
      if (problem[node.state][i] > 0) then
        if (i ~= node.state) then
          local child = {state = i}
          local path = {}
          for j = 1, #node.parent do
            table.insert(path, node.parent[j])
          end
          table.insert(path, node.state)
          child.parent = path
          child.cost = {node.cost[1] + problem[node.state][i],
            heuristic[i]}
          table.insert(successors, child)
        end
      end
    end
    if (#successors == 0) then
      return {state = 0}
    end
    while (true) do
      -- 1st and 2nd lowest fval in successors
      local best = successors[1]
      local alternative = best
      if (#successors > 1) then
        alternative = successors[2]
        if ((best.cost[1] + best.cost[2]) >
          (alternative.cost[1] + alternative.cost[2])) then
          best, alternative = alternative, best
        end
        for i = 3, #successors do
          -- check best
          if ((successors[i].cost[1] + successors[i].cost[2]) <
            (best.cost[1] + best.cost[2])) then
            alternative = best
            best = successors[i]
          elseif ((successors[i].cost[1] + successors[i].cost[2]) <
            (alternative.cost[1] + alternative.cost[2])) then
            alternative = successors[i]
          end
        end
      end
      local bestf = best.cost[1] + best.cost[2]
      local alternativef = alternative.cost[1] + alternative.cost[2]
      local result
      if (bestf < flimit) then
        result = rbfs(problem, best, finish, heuristic,
          math.min(flimit, alternativef))
      else
        node.cost[1] = best.cost[1]
        node.cost[2] = best.cost[2]
        return {state = 0}
      end
      if (result.state ~= 0) then
        return result
      end
    end
  end
end

Regarding its implementation, see Figure 2, the RBFS algorithm depicted in AIMA is somewhat puzzling and it does not take into account a scenario with one single successor. Note how the former code specifically tackles these issues so that the final algorithm behaves as expected.

With RBFS you made it to the end of chapter 3. Over the course of the former posts, you have reviewed some of the most practical search methods, which are able to solve many types of problems in AI like puzzles, robot navigation, or the famous travelling salesman problem. In addition, the language processing field is also in need of such search algorithms to solve problems in speech recognition, parsing, and machine translation. All these fancy applications will be targeted in due time. In the following posts, the idea of “classical” search you have seen so far will be generalised to cover a broader scope of state-spaces. Stay tuned!