Artificial Neural Networks are powerful models in Artificial Intelligence and Machine Learning because they are suitable for many scenarios. Their elementary working form is direct and simple. However, the devil is in the details, and these models are particularly in need of much empirical expertise to get tuned adequately so as to succeed in solving the problems at hand. This post intends to unravel these adaptation tricks in plain words, concisely, and with a pragmatic style. If you are a practitioner focused on the value-added aspects of your business and need to have a clear picture of the overall behaviour of neural nets, keep reading.
Note that the neural network is plausibly renown to be the universal learning system. Without loss of generality, the text below makes some decisions regarding the model shape/topology, the training method, and the like. These design choices, though, are easily tweaked so that the same implementation may be suitable to solve all kinds of problems. This is accomplished by first breaking down its complexity, and then by depicting a procedure to tackle problems systematically in order to quickly detect model flaws and fix them as soon as possible. Let’s say that the gist of this process is to achieve a “lean adaptation” procedure for neural networks.
Theory of Operation
Artificial Neural Networks (ANNs) are interesting models in Artificial Intelligence and Machine Learning because they are powerful enough to succeed at solving many different problems. Historical evidence of their importance can be found as most leading technical books dedicate many pages to cover them comprehensibly.
Overall, ANNs are general-purpose universal learners driven by data. They conform to the connectionist learning approach, which is based on an interconnected network of simple units. Such simple units, aka neurons, compute a nonlinear function over the weighted sum of their inputs. You will see this clearly with the equations below. Neural networks are expressive enough to fit to any dataset at hand, and yet they are flexible enough to generalise their performance to new unseen data. It is true, though, that neural networks are fraught with experimental details and experience makes the difference between a successful model and a skewed one. The following sections cover the essentials of their modus operandi without getting bogged down in the small details.
Framework
Some say that 9 out of 10 people who use neural networks apply a multilayer perceptron (MLP). A MLP is basically a feed-forward network with 3 layers (at least): an input layer, an output layer, and a hidden layer in between, see Figure 1. Thus, the MLP has no structural loops: information always flows from left (input)to right (output). The lack of inherent feedback saves a lot of headaches. Its analysis is totally straightforward given that the output of the network is always a function of the input, it does not depend on any former state of the model or previous input.
Figure 1. Framework of a multilayer perceptron. Its behaviour is defined by the weight of its connections, which is given by the values of its parameters, i.e., the thetas.
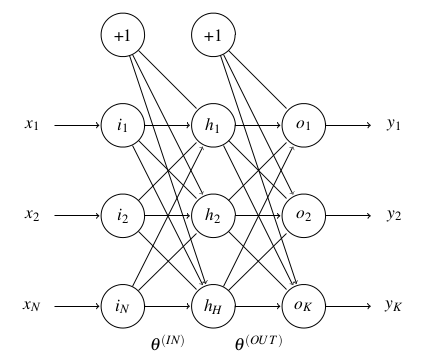
Regarding the topology of a MLP it is normally assumed to be a densely-meshed one-to-many link model between the layers. This is mathematically represented by two matrices of parameters named “the thetas”. In any case, if a certain connection is of little relevance with respect to the observable training data, the network will automatically pay little attention to its contribution and assign it a low weight close to zero.
Prediction
The evaluation of the output of a neural network, i.e., its prediction, given an input vector of data is a matter of matrix multiplication. To that end, the following variables are described for convenience:
- is the dimension of the input layer.
- is the dimension of the hidden layer.
- is the dimension of the output layer.
- is the dimension of the corpus (number of examples).
Given the variables above, the parameters of the network, i.e., the thetas matrices, are defined as follows:
The following sections describe the ordered steps that need to be followed in order to evaluate the network prediction.
Input Feature Expansion
The first step to attain a successful operation of the neural network is to add a bias term to the input feature space (mapped to the input layer):
The feature expansion of the input space with the bias term increases the learning effectiveness of the model because it adds a degree of freedom to the adaptation process. Note that directly represents the activation values of the input layer. Thus, the input layer is linear with the input vector (it is defined by a linear activation function).
Transit to the Hidden Layer
Once the activations (outputs) of the input layer are determined, their values flow into the hidden layer through the weights defined in :
Similarly, the dimensionality of the hidden layer is expanded with a bias term to increase its learning effectiveness:
Here, a new function is introduced. This is the generic activation function of a neuron, and generally it is non-linear, see below. Its application yields the output values of the hidden layer and provides the true learning power to the neural model.
Output Prediction
Finally, the activation values of the output layer, i.e., the network prediction, are calculated as follows:
Activation Function
The activation function of the neuron is a non-linear function that provides the expressive power to the neural network. Typically, the sigmoid function or the hyperbolic tangent function is used. It is recommended this function be smooth, differentiable and monotonically non-decreasing (for learning purposes).
Note that the range of these functions varies from to , respectively. Therefore, the output values of the neurons will always be bounded by the upper and the lower limits of these ranges. This entails considering a scaling process if a broader range of predicted values is needed.
Training
Training a neural network essentially means fitting its parameters to a set of example data considering an objective function, aka cost function. This process is also known as supervised learning. It is usually implemented as an iterative procedure.
Cost Function
The cost function somehow encodes the objective or goal that should be attained with the network. It is usually defined as a classification or a regression evaluation function. However, the actual form of the cost function is effectively the same, which is an error or fitting function.
The cost function quantifies the amount of error (or misfitting) that the network displays with respect to a set of data. Thus, in order to achieve a successfully working model, this cost function must be minimised with an adequate set of parameter values. To do so, several solutions are valid as long as this cost function be a convex function (i.e., a bowl-like shape). A well known example of such is the quadratic function, which trains the neural network considering a minimum squared error criterion over the whole dataset of training examples:
Note that the term in the cost function represents the target value of the network (i.e., the ideal/desired network output) for a given input data value . Now that the cost function can be expressed, a convex optimisation procedure (e.g., a gradient-based method) must be conducted in order to minimise its value. Note that this is essentially a least-squares regression.
One last remark should be made about the amount of examples . If the training procedure considers several instances at once per cost computation, i.e., , the approach is called batch learning. Batch learning is slow because each cost computation accounts for all the available training instances. In contrast, it is usual to consider only one training instance at a time, i.e., , in order to speed up the iterative learning process. This procedure is called online learning. Online learning steps are faster to compute, but this single-instance approximation of the cost function makes it a little inaccurate around the optimum. However, online learning is rather convenient in most cases.
Gradient Descent
Given the convex shape of the cost function, the minimisation objective boils down to finding the extremum of this function. To this end you may use the analytic form of the derivative of the cost function (a nightmare), a numerical finite difference, or automatic differentiation.
Gradient descent is a first-order optimisation algorithm. It first starts with some arbitrarily chosen parameters and computes the derivative of the cost function with respect to each of them. The model parameters are then updated by moving them some distance (determined by the so called learning rate) from the former initial point in the direction of the steepest descent, i.e., along the negative of the gradient. These steps are iterated in a loop until some stopping criterion is met, e.g., a determined number of epochs (i.e., the single presentation of all patterns in the training example set) is reached.
Gradient descent is effectively the same algorithm as gradient ascent, but seeking a minimum of the objective function instead of a maximum. In order to reuse the already developed code (recall the DRY – Don’t Repeat Yourself principle, tip number 11 from The Pragmatic Programmer), I’m going to take the negative of the former cost function like in order to conduct the gradient descent approach with the gradient ascent algorithm. Note that the algorithm needs a learning rate parameter, which sets the step size used to update the neural network model parameters. If it is set too small, convergence is needlessly slow, whereas if it is too large, the update correction process may overshoot and even diverge.
Parameter Initialisation
The initial weights of the thetas assigned by the training process are critical with respect to the success of the learning strategy. They determine the starting point of the optimisation procedure, and depending on their value, the adjusted parameter values may end up in different places if the cost function has multiple (local) minima.
The parameter initialisation process is based on a uniform distribution between two small numbers that take into account the amount of input and output units of the adjacent layers:
In order to ensure a proper learning procedure, the weights of the parameters need to be randomly assigned in order to prevent any symmetry in the topology of the network model (that would be likely to incur convergence problems).
Regularisation
The mean squared-error cost function described above does not incorporate any knowledge or constraint about the characteristics of the parameters being adjusted through the gradient descent optimisation strategy. This may develop into a generalisation problem because the space of solutions is large and some of these solutions may turn the model unstable with new unseen data. Therefore, there is the need to smooth the performance of the model over a wide range of input data.
Neural networks usually generalise well as long as the weights are kept small. This tip is also in concordance with the parameter initialisation. Thus, the Tikhonov regularisation process, aka ridge regression, is introduced as a means to control complexity of the model in favour of its increased general performance. This regularisation approach favours small weight values:
There is a typical trade-off in Machine Learning, known as the bias-variance trade-off, which has a direct relationship with the complexity of the model, the nature of the data and the amount of available training data to adjust it. This ability of the model to learn more or less complex scenarios raises an issue with respect to its fitting: if the data is simple to explain, a complex model is said to overfit the data, causing its overall performance to drop (high variance model). Similarly, if complex data is tackled with a simple model, such model is said to underfit the data, also causing its overall performance to drop (high bias model). As it is usual in engineering, a compromise must be reached with an adequate value.
Practical Issues
The success of Artificial Intelligence and Machine Learning applications is plausibly conceived as a matter of controlling several key variables and following a series of “good practices”. There are some works in the literature that identify the bits and pieces to be taken into account when designing a successful model. Some of these are described as follows:
- Focus on model generalisation: keep a separate self-validation set of data (not used to train the model) to test and estimate the actual performance of the model.
- Incorporate as much knowledge as possible. Expertise is a key indicator of success. Data driven models don’t do magic, the more information that is available, the greater the performance of the model.
- Feature Engineering is of utmost importance. This relates to the former point: the more useful information that can be extracted from the input data, the better performance can be expected. Salient indicators are keys to success. This may lead to selecting only the most informative features (mutual information, chi-square…), or to change the feature space that is used to represent the instance data (Principal Component Analysis…). And always standardise your data and exclude outliers.
- Get more data if the model is not good enough. Related to “the curse of dimensionality” principle: if good data is lacking, no successful model can be obtained. There must be a coherent relation between the parameters of the model (i.e., its complexity) and the amount of available data to train them.
- Ensemble models, integrate criteria. Bearing in mind that the optimum model structure is not known in advance, one of the most reasonable approaches to obtain a fairly good guess is to apply different models (with different learning features) to the same problem and combine/weight their outputs. Related techniques to this are also known as “boosting”.
The following sections delve into some of these topics with some practical strategies.
Target Values
When designing a learning system, it is suitable to take into account the nature of the problem at hand (e.g., whether if it is a classification problem or a regression problem) to determine the number of output units .
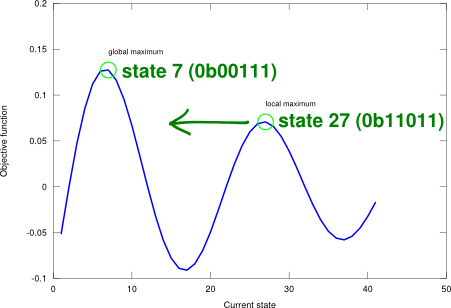
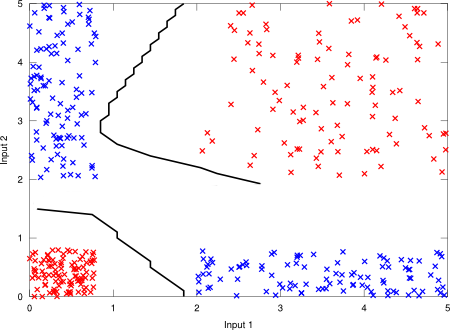
In the case of classification, should be the amount of different classes, and the target output should be a binary vector. Given an instance, only the output unit that corresponds to the instance class should be set. The decision rule for classification is then driven by the maximum output unit. Figure 2 shows a digital XOR gate with TTL technology (voltage thresholds are taken into account) with 2 inputs and 2 outputs (2 categories: “true” class or “false” class).
Figure 2. Digital XOR gate with TTL technology.
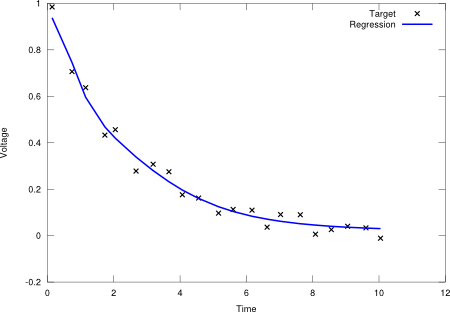
In the case of a regression problem, should be equal to the number of dependent variables. Figure 3 displays a regression over a capacitor discharge function (independent variable is time, dependent variable is voltage).
Figure 3. Capacitor discharge function.
Hidden Units
The number of hidden units determines the expressive power of the network, and thus, the complexity of its transfer function. The more complex a model is, the more complicated data structures it can learn. Nevertheless, this argument cannot be extended ad infinitum because a shortage of training data with respect to the amount of parameters to be learnt may lead the model to overfit the data. That’s why the aforementioned regularisation function is used to avoid this situation.
Thus, it is common to have a skew toward suggesting a slightly more complex model than strictly necessary (regularisation will compensate for the extra complexity if necessary). Some heuristic guidelines to guess this optimum number of hidden units indicate an amount somewhat related to the number of input and output units. This is an experimental issue, though. There is no rule of thumb for this. Apply a configuration that works for your problem and you’re done.
The end
Presently, there is hype about deep learning (i.e., like a rebranding of multilayer neural networks) as the next big thing in Machine Learning and Artificial Intelligence. However, until very recently, it was very hard to publish something in the scientific community about neural networks. Now the fashion is back and neural nets seem to be the fanciest technique that ever existed, and all problems seem to be solvable, especially when the size of the network grows to huge numbers (this is the era of big data, right?).
Figure 4. Artificial Neural Network.
-- Artificial neural network class (multilayer perceptron model).
--
-- Activation function is assumed to be sigmoid.
-- Tikhonov regularisation is set to 1.
ann = {}
-- PRE:
-- IN - size of input layer (number).
-- HID - size of hidden layer (number).
-- OUT - size of output layer (number).
--
-- POST:
-- Returns an instance of an ANN (table).
function ann:new(IN, HID, OUT)
local newann = {Lin = IN, Lhid = HID, Lout = OUT}
self.__index = self
setmetatable(newann, self)
newann:initw()
return newann
end
-- POST:
-- Initialises the model (the thetas).
function ann:initw()
local epsilonIN = math.sqrt(6) / math.sqrt(self.Lin + self.Lhid)
local epsilonOUT = math.sqrt(6) / math.sqrt(self.Lhid + self.Lout)
--
local function initmat(din, dout, value)
math.randomseed(os.time())
local mat = {}
for i = 1, dout do
local aux = {}
for j = 1, din do
table.insert(aux, ((math.random() - 0.5) / 0.5 ) * value)
end
table.insert(mat, aux)
end
return mat
end
--
self.thetain = initmat(self.Lin + 1, self.Lhid, epsilonIN)
self.thetaout = initmat(self.Lhid + 1, self.Lout, epsilonOUT)
end
-- PRE:
-- input - feat [1,N] vector (table).
--
-- POST:
-- Returns output [1,K] vector (table).
function ann:predict(input)
local function matprod(m1, m2)
local result = {}
-- init
for i = 1, #m1 do
local row = {}
for j = 1, #m2[1] do
table.insert(row, 0)
end
table.insert(result, row)
end
-- multiply
for i = 1, #m1 do
for j = 1, #m2[1] do
local prod = 0
for k = 1, #m1[1] do
prod = prod + m1[i][k] * m2[k][j]
end
result[i][j] = prod
end
end
return result
end
--
local function sigmoid(x)
local y = 1 / (1 + math.exp(-x))
return y
end
-- input must be a column [N,1] vector (table).
-- step 1
local aIN = {{1}}
for i = 1, #input do
table.insert(aIN, {input[i]})
end
-- step 2
local zHID = matprod(self.thetain, aIN)
local aHID = {{1}}
for i = 1, #zHID do
table.insert(aHID, {sigmoid(zHID[i][1])})
end
-- step 3
local azOUT = matprod(self.thetaout, aHID)
for i = 1, #azOUT do
azOUT[i][1] = sigmoid(azOUT[i][1])
end
local flatOUT = {}
for i = 1, #azOUT do
table.insert(flatOUT, azOUT[i][1])
end
return flatOUT
end
-- PRE:
-- feat - list of example feature vectors (table).
-- targ - list of target value vectors (table).
--
-- POST:
-- Fits the neural network params to the given data.
-- Returns training error (number).
function ann:train(feat, targ)
require("gradient_ascent")
local function saveThetas()
local thetas = {}
-- theta in
for i = 1, self.Lhid do
for j = 1, (self.Lin + 1) do
table.insert(thetas, self.thetain[i][j])
end
end
-- theta out
for i = 1, self.Lout do
for j = 1, (self.Lhid + 1) do
table.insert(thetas, self.thetaout[i][j])
end
end
return thetas
end
local function loadThetas(thetas)
-- theta in
local index = 1
for i = 1, self.Lhid do
for j = 1, (self.Lin + 1) do
self.thetain[i][j] = thetas[index]
index = index + 1
end
end
-- theta out
for i = 1, self.Lout do
for j = 1, (self.Lhid + 1) do
self.thetaout[i][j] = thetas[index]
index = index + 1
end
end
end
local function cost(thetas)
local sqerr, pr
local J = 0
loadThetas(thetas)
for m = 1, #feat do
pr = self:predict(feat[m])
sqerr = 0
for k = 1, #pr do
sqerr = sqerr + math.pow(targ[m][k] - pr[k], 2)
end
J = J + sqerr
end
J = J / #feat
-- Regularisation
local R = 0
for i = 1, #self.thetain do
for j = 2, #self.thetain[1] do
R = R + math.pow(self.thetain[i][j], 2)
end
end
for i = 1, #self.thetaout do
for j = 2, #self.thetaout[1] do
R = R + math.pow(self.thetaout[i][j], 2)
end
end
R = R * (0.01 / (self.Lin*self.Lhid + self.Lhid*self.Lout))
return -(J + R)
end
-- flatten thetas
local flatTheta = saveThetas()
gradient_ascent(cost, flatTheta, 1)
-- deflat theta, restore model
trerr = cost(flatTheta)
loadThetas(flatTheta)
-- return training err
return trerr
end
Neural networks are inherently hard per se, as they’ve always been. Getting them to succeed on a wide range of problems is a challenging task, indeed. However, their basic form of operation is simple. In fact, it is as simple as that of a plain (least squares) regression with a sophisticated fitting function. The complete code listing is shown in Figure 4. Actually, there exists a myriad of techniques to deal with many details (for example, the renown backpropagation learning algorithm), but without loss of generality, they have been left out of the scope aimed at this post (the big picture of neural nets). You’ll be reading about them in a future post in due time. Stay tuned!