The first topic that is tackled in the AIMA book is problem solving by searching over a graphical structure. The overall operation of this family of algorithms is based on traversing the given graph, keeping unexplored nodes in a container called the “frontier”, and then exploring these nodes, one at a time. The strategy to conduct the search process, thus, depends on how nodes are managed with the frontier. If the frontier is treated as a queue, i.e., First-In First-Out, then the graph traversal is progressed via a breadth-first criterion, whereas if the frontier is used as a stack, i.e., Last-In First-Out, then the search algorithm expands by depth-first.
There is another issue regarding the redundancy of the paths. If the search algorithm does not take into account which nodes it explores along the way, it may traverse them more than once. This is called a tree-search algorithm. Instead, if it makes sure to not traverse the same node twice, it is called a graph-search algorithm. The suitability of one or the other depends on the nature of the objective problem at hand (and the ability of the searcher to trace its own footsteps in case it reaches a dead end).
Also, some search algorithms operate with the support of some guiding knowledge (that is like a kind of compass that points to the right direction), which are called informed search strategies, while others go around blindly without any knowledge at all about what next action is best, which are called uninformed search strategies. What must be common to all problem definitions, though, is that the step costs from one node to another be non-negative.
Based on the former premises, several search routines are typically defined. What follows are the details of the breadth-first search (BFS) algorithm.
BFS in detail
Breadth-first is an uninformed search strategy that seeks the shallowest path to the solution. Since it uses a FIFO queue for the frontier, the nodes at a given depth are always expanded before any nodes at the next level. This algorithm is commonly implemented following a graph-search template, see Figure 1, also available on the GitHub repository.
Figure 1. Breadth-first search algorithm.
## @deftypefn {Function File} {@var{solution} =} breadth_first_search (@var{problem}, @var{start}, @var{finish})
## Breadth-first search on a graph.
##
## PRE:
## @var{problem} must be the cost-weighted adjacency matrix.
## @var{start} must be the starting node index.
## @var{finish} must be the finishing node index.
##
## POST:
## @var{solution} is the solution path. State set to zero if failure.
## @end deftypefn
## Author: Alexandre Trilla <alex@atrilla.net>
function [solution] = breadth_first_search(problem, start, finish)
% inits
node.state = start;
node.parent = [];
node.cost = 0;
if (node.state == finish)
solution = node;
else
frontier = [node];
explored = [];
found = 0;
while (~found)
if (numel(frontier) == 0)
solution.state = 0;
found = 1;
break;
endif
% pop frontier
node = frontier(1);
frontier = frontier(2:end);
% explore
explored(numel(explored)+1) = node.state;
for i = 1:size(problem, 2)
if (problem(node.state, i)>0)
if (i ~= node.state)
if (~sum(explored == i))
inFront = 0;
for j = 1:numel(frontier)
if (frontier(j).state == i)
inFront = 1;
break;
endif
endfor
if (~inFront)
% expand search space
child.state = i;
path = node.parent;
path = [path node.state];
child.parent = path;
child.cost = node.cost + ...
problem(node.state, i);
% check goal
if (i == finish)
solution = child;
found = 1;
break;
else
frontier = [frontier child];
endif
endif
endif
endif
endif
endfor
endwhile
endif
endfunction
The gist of the BFS approach is to explore all possible options at a given point/level before making a decision on what to do next (i.e., the following node to be explored). Thus, it’s kind of hesitant. This has important implications on the computational complexity of this algorithm. Both time and space complexities are exponential with respect to the branching factor , i.e., the number of nodes that the search tree generates at a given level, and the depth of the solution: . Therefore, memory requirements are a bigger problem for BFS than is the execution time. In general, exponential-complexity search problems cannot be solved by uninformed methods for any but the smallest instances.
As a practical example, let’s use the graphical map of Germany from Wikipedia, see Figure 2a. If you apply BFS from Frankfurt to München, for example, the algorithm resolves the problem via Kassel, which is the shallowest path (two hops), see Figure 2b. This is fine. However, this is by no means the least costly solution as the distance amounts to 675km: it is not optimum in this distance-cost sense.
Figure 2. BFS applied on the graphical map of Germany. Source: Wikipedia. a) Problem description. b) Search tree.
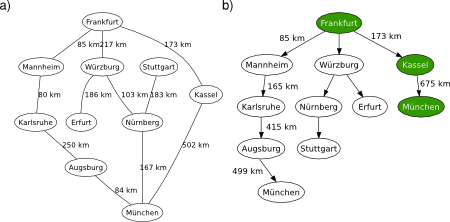
BFS may be somewhat misleading in this case because it treats physical dimensions as if they all weighed the same. But there is room for improvement here. So stay tuned for the next post. There you will deal with the optimum search strategy that accounts for the lowest-cost path to resolve the traversal of the graph.

6 thoughts on “Breadth-first search”
Comments are closed.