A genetic algorithm (GA) is a variant of stochastic beam search, which involves several search points/states concurrently (similar to the shotgun approach noted in the former post), and somehow combines their features according to their performance to generate better successor states. Thus, GA differs from former approaches like simulated annealing that only rely on the modification and evolution of a single state.

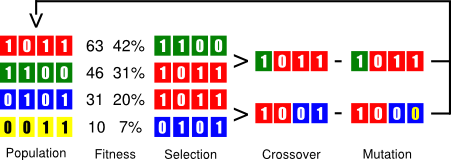
In GA, each search state, aka individual, encodes the problem information, usually as a binary array. GA begins with a set of randomly generated states, called the population. Then, it iterates over the chain of evolution for a determined number of rounds, see Figure 1, described as follows:

1. Fitness evaluation: each state is scored wrt some effectiveness criterion (higher values for better states).
2. Selection: states are randomly sampled with a specific probability according to their fitness value.
3. Crossover: selected individuals are randomly shuffled or combined at a specific point.
4. Mutation: child individuals may flip some of their bits (each one with independent probability).

Figure 1. Chain of evolution in genetic algorithms.

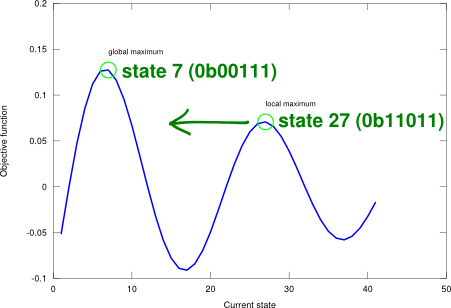
The advantage with GA comes from the ability of crossover to combine large blocks of bits (i.e., state information) that have evolved independently to perform a specific useful function. However, the successful use and application of GA requires careful engineering of the state representation and its encoding (in addition to the more common optimisation parameters like the population size or the number of evolution rounds). This has a deep impact on the performance of the algorithm. Figure 2 shows an example objective landscape where the state-space number is represented as a binary array of 5 bits (unsigned integer).

Figure 2. Genetic algorithm applied on a one-dimensional state-space landscape described by an example objective function .

GA belongs to a family of metaheuristics, which are algorithms designed to tackle ill-defined functions where a clear and definite objective is impossible to use. GA are adequate for black box search processes. Figure 3 implements the GA algorithm. Note how no explicit objective function is given. Instead, an initial population and a fitness function are passed to begin the search for the optimum.

Figure 3. Genetic algorithm.

-- Genetic algorithm.
--
-- PRE:
-- population - set of individuals (table).
-- fitness - evaluate individual (function).
--
-- POST:
-- solution - solution state (table).
--
-- Each individual (state) is a binary array.
-- Population is ordered from best to worst according to fitness. It
-- must be greater than one.
-- Fitness is normalised from 0 (bad) to 1 (good).

local function sort_population(population, fitness)
  local function comp(x, y)
    return (fitness(x) < fitness(y))
  end
  return table.sort(population, comp)
end

local function random_selection(population, fitness)
  local fit = {}
  local sumfit = 0
  for i = 1, #population do
    local fitIndi = fitness(population[i])
    table.insert(fit, fitIndi)
    sumfit = sumfit + fitIndi
  end
  fit[1] = fit[1] / sumfit
  for i = 2, #fit do
    fit[i] = fit[i] / sumfit + fit[i-1]
  end
  local x, y
  local rx = math.random()
  local ry = math.random()
  for i = 1, #fit do
    if (rx < fit[i]) then
      x = population[i]
      break
    end
  end
  for i = 1, #fit do
    if (ry < fit[i]) then
      y = population[i]
      break
    end
  end
  return x, y
end

local function reproduce(x, y)
  local point = math.floor(math.random() * #x) + 1
  local child = {}
  for i = 1, point do
    child[i] = x[i]
  end
  for i = point + 1, #x do
    child[i] = y[i]
  end
  return child
end

local function mutate(x)
  for i = 1, #x do
    if (math.random() < 0.1) then
      x[i] = math.abs(x[i] - 1)
    end
  end
end

function genetic_algorithm(population, fitness)
  local solution
  for epoch = 1, 100 do
    sort_population(population, fitness)
    local new_population = {}
    for i = 1, #population do
      local x, y = random_selection(population, fitness)
      local child = reproduce(x, y)
      if (math.random() < 0.05) then
        mutate(child)
      end
      table.insert(new_population, child)
    end
    population = new_population
  end
  return population[1]
end

The GA algorithm suggested in AIMA does not posit any similarity with real world reproductive systems, though. Is it reasonable to prevent inbreeding? In nature, close genetic relation results in disorders. Such issues are not discussed, but they don’t seem to have much of an impact for function optimisation purposes (in this particular case, mutation may add value here by creating a new individual).

Finally, regarding the computational complexities of GA, the space complexity is given by the number of individuals in the population , and the time complexity is given by the intermediate processes of the evolution chain. I guess one the critical points is ranking the individuals according to their fitness value for sampling. In the former implementation, Lua’s table.sort function (based on quicksort) is used. However, I would expect an overall for a tractable amount of instances. Depending on how fine you are with respect to your specific problem, several options may fit. Use your most sensible and plausible bound here (and test it!).