
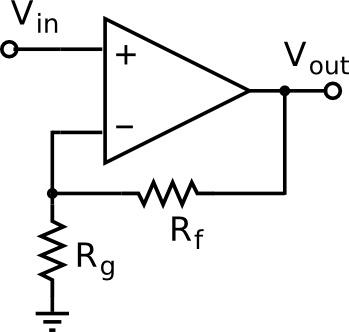
Encoding problem state information in a genetic algorithm (GA) is one of the most cumbersome aspects of its deployment. GA deals with binary vectors, so this is the format that you must comply to in order to find optimum solutions with this technique. And depending on which strategy you choose to do it, the solution of the search process may be different, and/or the GA algorithm may take more or less time (and/or space) to reach it. In order to display some of these issues, I will go through a complete example with an electronic circuit in this post. Specifically, the circuit under analysis will be a non-inverting amplifier built with an OP07 operational amplifier, see Figure 1. The goal of this discrete optimisation problem will be to find the optimum values of its two resistors Rf and Rg (over a finite set, so that they may be available in the store and the circuit be implementable) that maximise the symmetric excursion of a 1V peak input sinusoidal signal without clipping. Let’s synthesise this circuit with GA!
Figure 1. Schematic of a non-inverting amplifier. Source: Wikipedia.
First step: encode each resistor value alone into a binary array. It is a good approach to represent the bits of an integer number, where the weight of each bit is directly related to a specific weight of the resistive spectrum, i.e., the most significant bits always correspond to high resistor values (and vice-versa), see Figure 2. I had also tried to follow the colour-based encoding that resistors display, i.e., like a mantissa and an exponent, but it’s been much of a failure, which I suspect is given by the non-linear relation between bit weight and resistance value. Note that you must still check that the represented number is within the accepted range of resistor values. Otherwise, discard it by assigning a bad fitness score so that it is likely to disappear during the evolution process. In this example, I’ll be using the 10% standard resistor values, from 10 ohm to 820k ohm (so, 60 different values in total, 6 bits).
Figure 2. Resistor value encoding and crossover.
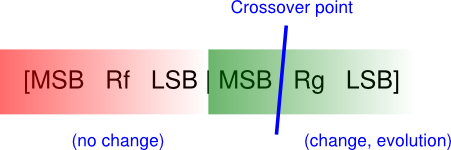
Next, encode the two resistor values in an array to create an initial population. To this end, append one resistor to the other to build an aggregate individual, like [Rf Rg], again see Figure 2. When having to combine them, the crossover point will keep the value of one resistor stable while evolving the other under improvement, which makes perfect sense.
Now, the output function of the non-inverting amplifier is given by:
and the fitness function used to evaluate the effectiveness of a solution is mainly driven by the inverse of the error of the symmetric excursion of (recall that greater scores are for better individuals):
Taking into account that with a power supply of 15V the OP07 saturates at about 12V, let’s fix the maximum symmetric excursion of the output to 20V (i.e., ) to avoid signal clipping. Having all that set, you’re ready to start optimising. Having a look at the fitness surface that the GA algorithm will deal with, see Figure 3, it shows that it will have a hard time dealing with so many extrema. Note that all maxima are located on a 9x slope line, which indicates that the solution must maintain a ratio of 9 between Rf and Rg. Also note that resistors placed on the lower end of the resistance range tend to be more stable and consume more power, while the ones placed on the higher end of the range draw less current but are more unstable. Since none of these considerations are included in the fitness function, the GA procedure may end on any of these local maxima, e.g, and , with a fitness score of .
Figure 3. Fitness surface plot.

The performance of a brute-force exhaustive iterative search solution is taken for reference here, which has a computational complexity in time of , where is amount of possible resistor values (i.e., 60), and is the number of resistors in circuit (i.e., 2). This yields a search space of 3600 states. No matter how fancy GA’s may be, for such small search space, exhaustive linear search is much faster (it takes less than a second, while GA takes 5 secs). With 4 resistors, though, the search space is over 12M and the two approaches take about 10 secs. Over this bound, GA is able to perform better. Long are the days when engineers had to assemble the prototype circuits on a breadboard to optimise the numerical values of each of the components, see this video at 6:15.
